Photonic topological insulators
 Photonic topological insulators are dielectric crystals that are endowed, by virtue of their complex structure, with protection against disorder. This “topological protection” arises for very deep reasons having to do with the topology of the photonic states of the structure. This means that light can propagate within materials perfectly, despite arbitrarily big defects. This can potentially have a range of applications, including producing higher-yield, lower-cost photonic devices that can push deeper into the nanophotonic domain. This property can also be used to overcome fundamental trade-offs in photonics: Specifically, these ideas can be used to achieve very slow propagation of light over large bandwidths, while simultaneously being insensitive to disorder, a holy grail in photonics. When light propagates slowly, it interacts more strongly with the ambient material, and can thus be used to more efficiently generate quantum states of light, on-chip supercontinua, and ultrasmall laser sources. Photonic topological insulators are dielectric crystals that are endowed, by virtue of their complex structure, with protection against disorder. This “topological protection” arises for very deep reasons having to do with the topology of the photonic states of the structure. This means that light can propagate within materials perfectly, despite arbitrarily big defects. This can potentially have a range of applications, including producing higher-yield, lower-cost photonic devices that can push deeper into the nanophotonic domain. This property can also be used to overcome fundamental trade-offs in photonics: Specifically, these ideas can be used to achieve very slow propagation of light over large bandwidths, while simultaneously being insensitive to disorder, a holy grail in photonics. When light propagates slowly, it interacts more strongly with the ambient material, and can thus be used to more efficiently generate quantum states of light, on-chip supercontinua, and ultrasmall laser sources.
|
Solitons in topological photonics
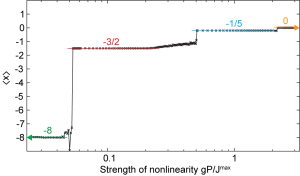 We have recently been really interested in the interplay between topological protection and nonlinearity/interactions of photons. This is really a new domain of exploration: so much interacting topological physics has been explored in the context of electrons (think fractional quantum Hall), but very little for photons, and bosons more broadly. In the high photon number (i.e., mean-field) regime, dynamics are governed by the focusing nonlinear Schrödinger equation (also referred as the attractive Gross-Pitaevskii equation). In a series of papers, we predicted an experimentally observed solitons in photonic topological insulators for the first time. Solitons are localized wavepackets that balance diffraction and nonlinearity to remain localized indefinitely: in other words, they’re nonlinear eigenstates. We’ve explored the interesting dynamics of bulk and chiral edge state solitons both theoretically and experimentally. In a surprise, we found that in nonlinear Thouless pumps, soliton motion can be quantized: we can actually think of this as a kind of nonlinear topological invariant. In the strongly nonlinear case, that quantization can even be fractional, evoking the interacting dynamics of the fractional quantum Hall effect (although the underlying physics is very different in the two cases). We have recently been really interested in the interplay between topological protection and nonlinearity/interactions of photons. This is really a new domain of exploration: so much interacting topological physics has been explored in the context of electrons (think fractional quantum Hall), but very little for photons, and bosons more broadly. In the high photon number (i.e., mean-field) regime, dynamics are governed by the focusing nonlinear Schrödinger equation (also referred as the attractive Gross-Pitaevskii equation). In a series of papers, we predicted an experimentally observed solitons in photonic topological insulators for the first time. Solitons are localized wavepackets that balance diffraction and nonlinearity to remain localized indefinitely: in other words, they’re nonlinear eigenstates. We’ve explored the interesting dynamics of bulk and chiral edge state solitons both theoretically and experimentally. In a surprise, we found that in nonlinear Thouless pumps, soliton motion can be quantized: we can actually think of this as a kind of nonlinear topological invariant. In the strongly nonlinear case, that quantization can even be fractional, evoking the interacting dynamics of the fractional quantum Hall effect (although the underlying physics is very different in the two cases).
|
Weyl 3D photonic crystals
 We’ve used two-photon polymerization (via the Nanoscribe tool) to fabricate complex 3D photonic crystals, such as those exhibiting Weyl points – topologically protected degeneracies in a band structure. In a series of works, we realized Weyl points for the first time, observed them in the mid-infrared frequency regime, and showed how a “charge-2” Weyl point can split up into two charge-1 Weyl points by perturbing the structure. We use a combination of theoretical techniques including group-theory based symmetry analysis, numerical techniques such as rigorous coupled wave analysis, and experimental techniques such as Fourier transform infrared spectroscopy in order to design and directly characterize the Weyl photonic cyrstals. We’ve used two-photon polymerization (via the Nanoscribe tool) to fabricate complex 3D photonic crystals, such as those exhibiting Weyl points – topologically protected degeneracies in a band structure. In a series of works, we realized Weyl points for the first time, observed them in the mid-infrared frequency regime, and showed how a “charge-2” Weyl point can split up into two charge-1 Weyl points by perturbing the structure. We use a combination of theoretical techniques including group-theory based symmetry analysis, numerical techniques such as rigorous coupled wave analysis, and experimental techniques such as Fourier transform infrared spectroscopy in order to design and directly characterize the Weyl photonic cyrstals.
|
Theory of topological structures
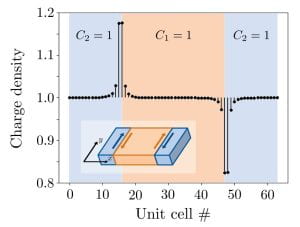 We study a range of theoretical problems in lattice systems, including in topological materials. In a recent work by graduate student Sachin Vaidya (who has moved on to a postdoc at MIT) and postdoctoral fellow Wladimir Benalcazar (currently a professor at Emory University), we showed that Chern insulators can have a well defined polarization. This is far from obvious because Chern insulators are – despite the name – actually metallic when in a finite system surrounded by vacuum, due to the presence of conducting edge states. By effectively surrounding the Chern insulator with others of the same Chern number, these conducting channels gap out and polarization can be defined through the presence of edge and corner states, as well as through the current induced by adiabatic (Thouless) pumping. We study a range of theoretical problems in lattice systems, including in topological materials. In a recent work by graduate student Sachin Vaidya (who has moved on to a postdoc at MIT) and postdoctoral fellow Wladimir Benalcazar (currently a professor at Emory University), we showed that Chern insulators can have a well defined polarization. This is far from obvious because Chern insulators are – despite the name – actually metallic when in a finite system surrounded by vacuum, due to the presence of conducting edge states. By effectively surrounding the Chern insulator with others of the same Chern number, these conducting channels gap out and polarization can be defined through the presence of edge and corner states, as well as through the current induced by adiabatic (Thouless) pumping.
|
New designs for endoscopes
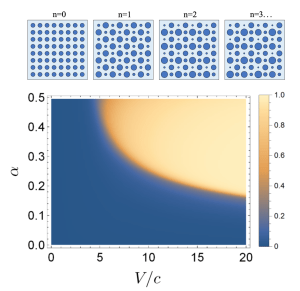 Endoscopes are medical imaging devices that transport images through the body through bundles of optical fiber. Contemporary designs use lossy glass to mitigate cross-talk (coupling) between neighboring fibers, which would otherwise blur the image. Unfortunately the loss that is introduced degrades the signal. Another idea that doesn’t employ loss is to use destructive interference to confine light – i.e., to prevent it from spreading. With graduate student Jonathan Guglielmon (who, after turning down a postdoc position at Stanford went to work at Analog Photonics in Boston), we showed that fractal designs are optimal for fiber-bundle based endoscopes. In a lattice that turned out to be highly reminiscent of the 2D Aubry-Andre model, we showed that after a sharp localization transition, the modes are exceedingly well localized and thus maintain high resolution with low loss. Endoscopes are medical imaging devices that transport images through the body through bundles of optical fiber. Contemporary designs use lossy glass to mitigate cross-talk (coupling) between neighboring fibers, which would otherwise blur the image. Unfortunately the loss that is introduced degrades the signal. Another idea that doesn’t employ loss is to use destructive interference to confine light – i.e., to prevent it from spreading. With graduate student Jonathan Guglielmon (who, after turning down a postdoc position at Stanford went to work at Analog Photonics in Boston), we showed that fractal designs are optimal for fiber-bundle based endoscopes. In a lattice that turned out to be highly reminiscent of the 2D Aubry-Andre model, we showed that after a sharp localization transition, the modes are exceedingly well localized and thus maintain high resolution with low loss.
|
Disorder and hyperuniformity
Coming soon… |
Pseudomagnetism: Landau levels for photons
Coming soon… |